QCD and the structure of matter
Atoms are like small solar systems: lots of empty space!
|
|
| Fig 1. An atom. Protons are colored red with a "+" charge. Neutrons are green with no charge. Electrons are blue with a "-" charge. |
A little less than a century ago, a series of table-top experiments conducted by Rutherford changed the way we understand the structure of matter. By observing rare but large deflections of high energy ionized helium gas particles impounding upon thin foils of gold, we understood that the building blocks of matter (atom) resembles our Solar System: most of the atom is empty and in the center of the atom there is a tiny core (called the nucleus) about 10000 times smaller than the atom, carrying almost all of the mass of the atom. This nucleus is made up of positively charged particles (called protons) and some slightly heavier electrically neutral particles (called neutrons). The atom looks like the adjacent figure: red circles are the positively charged protons, green ones are electrically neutral neutrons and the blue circles represent negatively charged electrons flying around the nucleus. There is an equal number of protons in the nucleus as the electrons (which are almost 2000 times lighter than the protons), and these electrons are bound to the atom by the electrical attraction from the positively charged nucleus.
A new "strong force"!
This picture led the curious to wonder:
we know that oppositely charged particles attract,
but particles with same charge repel each other;
so how do all those protons in the nucleus stay together without flying apart?
There must be some new kind of a force binding them together!
Thus, physicists conjured the existence of a new force
and called it the strong force. This strong force
binds both the protons and neutrons (collectively called nucleons)
together inside the nucleus.
The strong force is uniform inside the nucleus
The total binding energy per nucleon of any nucleus, ie. the mass of the
nucleus accurately measured, and subtracted from the sum of the masses
of the constituent nucleons, and divided by the number of the nucleons,
actually decreases as one goes to heavier nuclei. This suggests that
the attractive power of the strong force between the nucleons is roughly
constant inside the nucleus, while the electrical repulsion between the
nucleons increases with larger number of nucleons in the nuclei, eventually
leading to the instability of heavier nuclei.
Particles stuck in a well can tunnel out
|
|
| Fig 2. A nucleus is like a well, but particles inside can tunnel out. |
Physicists think of the particles in a nucleus as if they are stuck in a well that has
a slope outside the nucleus. If the particle has only enough energy to get half-way up the well,
physicists used to think it was trapped there forever, and could not get out. However,
a revolution in physics called Quantum Mechanics uncovered that the location
of a particle has an uncertainty to it related to its velocity.
This is referred to as the Uncertainty Principle.
For instance, there is an extremely small probability that some
of the particles in your body are in another country right now for an extremely
small period of time. Over time those chances add up.
For particles inside the nucleus, these odds really do add up to significant numbers
over the time scale of a typical laboratory experiment.
In other words, particles can sometimes tunnel out
through the walls if you watch them long enough.
For instance, there is an extremely small probability that some of the particles in your body are in another country right now for an extremely small period of time. Over time those chances add up. For particles inside the nucleus, these odds really do add up to significant numbers over the time scale of a typical laboratory experiment. In other words, particles can sometimes tunnel out through the walls if you watch them long enough.
Strong force is "short ranged"
Large unstable nuclei do not just spit out its constituent nucleons,
but each nuclei has its own characteristic emission signature (like positively charged
alpha particles).
This emission was explained (1928) by the Quantum Mechanical tunneling phenomenon.
By studying the rate of such emissions and its associated energy spectra from many nuclei,
physicists could guess the shape of the force field the alpha particles have to travel through.
Far away from the nucleus, as shown in the illustration above, the field decreases like a ramp
(which is exactly the behavior we expect from our ever familiar long ranged force
of electrical repulsion between the positively charged nucleus and the alpha particle).
As this force field is mapped closer and closer toward the nucleus,
it was discovered to have a sharp edge (corresponding to the boundary of the nucleus)
and a deep square well confining behavior inside the nucleus,
ascribed to be the domain of the strong force.
Thus we understand that the strong force is short ranged:
it operates at distances smaller than the size of the nucleus
(conventionally expressed in units of 1 Fermi which is about 10-15m).
How do they all stick together?
During early attempts to understand how the strong force binds the nucleons,
it was hypothesized that the proton and the neutron exchange some massive particle
between each other, like basketball players passing a basketball and thereby staying together
in the basketball court: someone has to throw and someone has to receive! The heavier
the ball thrown around, the closer the players have to be to each other
and thus be bound to the basketball court.
Yukawa predicted (1935) the mass of such a particle
exchanged to be roughly (1/10)th of the mass of the proton
based on the size of the nucleus (taken as an estimate of the range of the strong force).
Twelve years later (1947) by exposing photographic emulsion plates
on mountain tops to the cosmic rays, this particle (now called the pion)
was discovered having all the requirements of Yukawa's prediction.
In 1948, the first man-made charged pions were produced,
and neutral ones were discovered in 1950.
In the decade that followed (50's) many more strongly interacting particles were discovered.
A simple pion-exchange mechanism that seemed to work between the protons and the neutrons could not
explain the strong interaction between all these new particles discovered.
We now understand that the pion is a composite particle made up of quarks, as are the protons
and the neutrons, and the strong force describes the interaction between these quarks; but
Yukawa's theory was a major step in our advancement toward understanding
the nature of the strong force.
Discovery of the quarks
In 1968, electron-proton scattering
experiments were performed at SLAC, similar in spirit to the Rutherford
scattering experiments, but at a much higher energy scale. From the observed
pattern of rare large angle scattering of the electrons, physicists concluded that the
protons are made up of 3 compact particles called quarks.
The quarks are found to have 2 allowed polarization states. Now, there is an
old theorem that says particles with spin s can have 2s+1 allowed
polarization states. Thus physicists concluded that the quarks are spin 1/2
particles, explaining the 2*(1/2)+1 = 2 spin states.
Fractions all add up
All known matter participating in the strong interaction (generically referred to as hadrons)
are either electrically charged or neutral. They are found to have electric charge =
+2, +1, 0, -1, -2 .
To explain the observed pattern of mass and charge of all the known hadrons,
they are understood to be made up of two quarks (classified as mesons) or
three quarks (classified as baryons).
This pattern still works in explaining all the hadrons discovered till date,
but only if we assign fractional charges to the quarks.
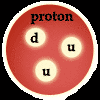

The proton with charge +1 is made up from 2 quarks with charge +2/3 each and
1 quark with charge -1/3, and the neutron with charge 0 is made up of 1 quark with
charge +2/3 and 2 quarks with charge -1/3 each.
The quark with charge +2/3 is given the name up quark (abbreviated as u) and
the quark with charge -1/3 is given the name down quark (abbreviated as d).
Thus the proton has quark signature uud, and the neutron's quark signature is udd.
The d quark is found to be slightly heavier than the u quark
explaining why the neutron is slightly heavier than the proton.
Generations of quarks
The two quarks (d and u) are said to form the first generation of quarks.
Since then, physicists have discovered 2 more generation of quarks:
each generation has a quark with charge -1/3 and another quark with charge +2/3.
These new quarks are called: strange and charm
(discovered in 1974), beauty or bottom (discovered in 1977) and truth or
top (discovered in 1995).
Color of quarks
Physicists initially thought that all the u and the d
quarks were identical, but the quarks have a strange property that do not
allow two identical ones to co-exist together in the same quantum state. This
property is much like that of electrons, which we know also have spin quantum
number = 1/2 and thus share the same statistical property called Pauli's
exclusion principle: no two of them can share the same quantum state.
As a consequence of this spin-statistics theorem, an odd number of
identical spin 1/2 quarks cannot be combined to form a
completely symmetric state.
Fermi discovered (1951) a particle
called a Delta++ carrying charge +2, which took part in the strong
interactions. Natural adding up of the charge and the mass of the
constituent quarks suggested that Delta++ is made up of 3 u quarks, but
this was a completely symmetric state (uuu) in contradiction with Pauli's
exclusion principle!
Physicists resolved this issue by introducing a
new quantum number called color charge to label the quarks. To allow three
otherwise identical u quarks to co-exist in Delta++, the color charge of
the quarks had to be of at least three types. Thus, one could for example
individually label the two otherwise identical u quarks in a proton to have
distinct color charges, and also allow three otherwise identical u quarks
with different color charges to co-exist in Delta++ without violating the
spin-statistics theorem.
This factor of three was actually a great
boon. The observed rate of quark anti-quark pair production from electron
anti-electron (called positron) annihilation was falling short of naive
expectations by exactly this factor of three. Allowing quarks to be of three
types varying in color solved that mystery as well.
Borrowing
terminology from common knowledge, physicists say that the quarks come in
three colors: red (R), blue (B) or green (G). (This color has nothing
whatsoever to do with the real color in everyday life: it just provides
labels for three distinct quantum states). Anti-quarks are given
the anti-colors of anti-red (anti-R), anti-blue (anti-B), and anti-green (anti-G).
Color Confinement
It has been found that all observed particles in Nature are color neutral.
Thus, the mesons are formed out of combinations of quarks with color charge:
(R and anti-R), or (B and anti-B), or (G and anti-G),
and the baryons are formed out of combinations like: (RBG) or (anti-R anti-B anti-G).
A free quark with its bare color charge can not be observed,
because if one tries to pull apart a color neutral hadron,
new hadrons are produced which are again color neutral.
This phenomena of color confinement actually has an analogue to an already
known phenomena in electro-magnetism (although the analogy is not exact,
it is useful in understanding the general behavior).
If we try to break a magnet (with N-pole S-pole pair)
we produce 2 magnets (each with its own N-pole S-pole pair) instead of
producing magnets with single pole by itself. Similarly, when we try to
"break" a color neutral hadronic particle, Nature produces more color neutral
hadronic particles each with its color and anti-color charge pairwise neutralized.
"Glue 'em up"
Fig 3. Two quarks exchange a gluon. The anti-red quark is represented by its
anti-color analogy of cyan. The gluon has two colors, blue and anti-red,
allowing the two quarks to interact.
From the 3 colored states allowed for quarks, one can form 9 bicolor states:
R anti-R, R anti-B, R anti-G, B anti-R, B anti-B, B anti-G, G anti-R, G anti-B, G anti-G.
Quarks interact amongst each other by exchange of such bicolor states called gluons
(which bind together the quarks!).
But, since the state (B anti-B + R anti-R + G anti-G) is a colorless combination,
there are only 8 bicolor states available for these gluons to exchange color between the quarks.
Discovery of the gluons
Direct experimental evidence of the gluon was first obtained at PETRA electron-positron
collider in 1979, where emission of a gluon from two quarks left measurable signature
in the experimental apparatus, distinct from the signatures of the two quarks themselves.
Our familiar understanding of the theory of electromagnetism,
called Quantum Electrodynamics (QED), is that there is only one mediator
of the interaction which is the photon, without any electric charge of its own.
One of the most remarkable feature of the theory of strong interaction,
called Quantum Chromodynamics (QCD), is that there are eight mediators of the interaction
which are the gluons, each carrying its own bicolor charge signature
and capable of emitting more gluons!
This has very interesting consequences ...
"Screens around electrons"
Fig 4. An electron sets up a screen making it
look more charged when you get close to it.
An electron in the quantum theory can spontaneously emit photons (for
a very short time), and these photons may form electron-positron pairs,
before they are absorbed back into the original electron. Thus if we probe
at very short distances (or equivalently at very high energies),
the original electron becomes surrounded by lots of such pairs with more
positive charges pointing toward itself (as illustrated in the diagram on the right).
As a result, the "effective electric charge of the electron" grows rapidly
when probed closer and closer to the electron (with higher and higher energy probes).
In the language of quantum theory,
physicists say that the vacuum around the electron has become highly polarized:
a phenomenon known as charge screening.
"Un-glue the quarks!"
Fig 5. Quarks screen themselves, but actually
seem to have less color the closer you get.
In QCD, the gluons emitted from a quark when probed at very short distances
(shorter than the range of the strong force) not only creates quark
anti-quark pairs but also emits more gluons with different bicolor signatures.
An illustrative diagram is shown on the right:
a red colored quark becomes surrounded by many bicolor gluons,
but preferentially with more red colored charges pointing toward itself as the other
color anti-color charged pairs cancel each other!
The net effect is a reversal of color charge screening,
and the "effective color charge of the quark" actually decreases with larger energy scale
(probing closer to the quark).
During early attempts to understand how the strong force binds the nucleons,
it was hypothesized that the proton and the neutron exchange some massive particle
between each other, like basketball players passing a basketball and thereby staying together
in the basketball court: someone has to throw and someone has to receive! The heavier
the ball thrown around, the closer the players have to be to each other
and thus be bound to the basketball court.
Yukawa predicted (1935) the mass of such a particle
exchanged to be roughly (1/10)th of the mass of the proton
based on the size of the nucleus (taken as an estimate of the range of the strong force).
Twelve years later (1947) by exposing photographic emulsion plates
on mountain tops to the cosmic rays, this particle (now called the pion)
was discovered having all the requirements of Yukawa's prediction.
In 1948, the first man-made charged pions were produced,
and neutral ones were discovered in 1950.
In the decade that followed (50's) many more strongly interacting particles were discovered.
A simple pion-exchange mechanism that seemed to work between the protons and the neutrons could not
explain the strong interaction between all these new particles discovered.
We now understand that the pion is a composite particle made up of quarks, as are the protons
and the neutrons, and the strong force describes the interaction between these quarks; but
Yukawa's theory was a major step in our advancement toward understanding
the nature of the strong force.
In 1968, electron-proton scattering
experiments were performed at SLAC, similar in spirit to the Rutherford
scattering experiments, but at a much higher energy scale. From the observed
pattern of rare large angle scattering of the electrons, physicists concluded that the
protons are made up of 3 compact particles called quarks.
The quarks are found to have 2 allowed polarization states. Now, there is an
old theorem that says particles with spin s can have 2s+1 allowed
polarization states. Thus physicists concluded that the quarks are spin 1/2
particles, explaining the 2*(1/2)+1 = 2 spin states.
All known matter participating in the strong interaction (generically referred to as hadrons)
are either electrically charged or neutral. They are found to have electric charge =
+2, +1, 0, -1, -2 .
To explain the observed pattern of mass and charge of all the known hadrons,
they are understood to be made up of two quarks (classified as mesons) or
three quarks (classified as baryons).
This pattern still works in explaining all the hadrons discovered till date,
but only if we assign fractional charges to the quarks.


The proton with charge +1 is made up from 2 quarks with charge +2/3 each and
1 quark with charge -1/3, and the neutron with charge 0 is made up of 1 quark with
charge +2/3 and 2 quarks with charge -1/3 each.
The quark with charge +2/3 is given the name up quark (abbreviated as u) and
the quark with charge -1/3 is given the name down quark (abbreviated as d).
Thus the proton has quark signature uud, and the neutron's quark signature is udd.
The d quark is found to be slightly heavier than the u quark
explaining why the neutron is slightly heavier than the proton.
The two quarks (d and u) are said to form the first generation of quarks.
Since then, physicists have discovered 2 more generation of quarks:
each generation has a quark with charge -1/3 and another quark with charge +2/3.
These new quarks are called: strange and charm
(discovered in 1974), beauty or bottom (discovered in 1977) and truth or
top (discovered in 1995).
Physicists initially thought that all the u and the d
quarks were identical, but the quarks have a strange property that do not
allow two identical ones to co-exist together in the same quantum state. This
property is much like that of electrons, which we know also have spin quantum
number = 1/2 and thus share the same statistical property called Pauli's
exclusion principle: no two of them can share the same quantum state.
As a consequence of this spin-statistics theorem, an odd number of
identical spin 1/2 quarks cannot be combined to form a
completely symmetric state.
Fermi discovered (1951) a particle
called a Delta++ carrying charge +2, which took part in the strong
interactions. Natural adding up of the charge and the mass of the
constituent quarks suggested that Delta++ is made up of 3 u quarks, but
this was a completely symmetric state (uuu) in contradiction with Pauli's
exclusion principle!
Physicists resolved this issue by introducing a
new quantum number called color charge to label the quarks. To allow three
otherwise identical u quarks to co-exist in Delta++, the color charge of
the quarks had to be of at least three types. Thus, one could for example
individually label the two otherwise identical u quarks in a proton to have
distinct color charges, and also allow three otherwise identical u quarks
with different color charges to co-exist in Delta++ without violating the
spin-statistics theorem.
This factor of three was actually a great
boon. The observed rate of quark anti-quark pair production from electron
anti-electron (called positron) annihilation was falling short of naive
expectations by exactly this factor of three. Allowing quarks to be of three
types varying in color solved that mystery as well.
Borrowing
terminology from common knowledge, physicists say that the quarks come in
three colors: red (R), blue (B) or green (G). (This color has nothing
whatsoever to do with the real color in everyday life: it just provides
labels for three distinct quantum states). Anti-quarks are given
the anti-colors of anti-red (anti-R), anti-blue (anti-B), and anti-green (anti-G).
It has been found that all observed particles in Nature are color neutral.
Thus, the mesons are formed out of combinations of quarks with color charge:
(R and anti-R), or (B and anti-B), or (G and anti-G),
and the baryons are formed out of combinations like: (RBG) or (anti-R anti-B anti-G).
A free quark with its bare color charge can not be observed,
because if one tries to pull apart a color neutral hadron,
new hadrons are produced which are again color neutral.
This phenomena of color confinement actually has an analogue to an already
known phenomena in electro-magnetism (although the analogy is not exact,
it is useful in understanding the general behavior).
If we try to break a magnet (with N-pole S-pole pair)
we produce 2 magnets (each with its own N-pole S-pole pair) instead of
producing magnets with single pole by itself. Similarly, when we try to
"break" a color neutral hadronic particle, Nature produces more color neutral
hadronic particles each with its color and anti-color charge pairwise neutralized.
From the 3 colored states allowed for quarks, one can form 9 bicolor states: R anti-R, R anti-B, R anti-G, B anti-R, B anti-B, B anti-G, G anti-R, G anti-B, G anti-G. Quarks interact amongst each other by exchange of such bicolor states called gluons (which bind together the quarks!). But, since the state (B anti-B + R anti-R + G anti-G) is a colorless combination, there are only 8 bicolor states available for these gluons to exchange color between the quarks.
Direct experimental evidence of the gluon was first obtained at PETRA electron-positron
collider in 1979, where emission of a gluon from two quarks left measurable signature
in the experimental apparatus, distinct from the signatures of the two quarks themselves.
Our familiar understanding of the theory of electromagnetism,
called Quantum Electrodynamics (QED), is that there is only one mediator
of the interaction which is the photon, without any electric charge of its own.
One of the most remarkable feature of the theory of strong interaction,
called Quantum Chromodynamics (QCD), is that there are eight mediators of the interaction
which are the gluons, each carrying its own bicolor charge signature
and capable of emitting more gluons!
This has very interesting consequences ...
An electron in the quantum theory can spontaneously emit photons (for a very short time), and these photons may form electron-positron pairs, before they are absorbed back into the original electron. Thus if we probe at very short distances (or equivalently at very high energies), the original electron becomes surrounded by lots of such pairs with more positive charges pointing toward itself (as illustrated in the diagram on the right). As a result, the "effective electric charge of the electron" grows rapidly when probed closer and closer to the electron (with higher and higher energy probes). In the language of quantum theory, physicists say that the vacuum around the electron has become highly polarized: a phenomenon known as charge screening.
Thus, on one hand, gluons un-glue the quarks (and nucleons deep inside the nucleus of an atom)
when they are very close to each other (or equivalently at very high energies),
and on the other hand, they glue together the quarks (forming the edge of the nucleus)
when the quark tries to move away from other quarks.
This variation of color charge with respect to the distance at which the quark is probed
is illustrated in the Figure 6: at distances of about a Fermi, the force between the
color charges confine the quarks to within the boundary of the nucleus, while at very short
distances the quarks do not feel the color force from any particular color charge and behave as if
they are almost free!
"... and never the twain shall meet?"
The strength of QED, as we saw above, increases with energy. In contrast,
the strength of QCD decreases with energy.
Our present understanding of the particle interactions is in terms of three kinds of forces:
the electromagnetic force, the weak force, and the strong force.
Together this description is called the Standard Model (SM) of particle physics.
The energy evolution of the strength of these forces
can be extrapolated to very high energies
from their measured values at presently accessible energy ranges.
Schematic representation of these extrapolations are illustrated on the left
plot (figure 7)
for the strength of electro-magnetic (aEM),
weak (aW) and
strong (aS)
interactions.
Our present understanding of the particle interactions is in terms of three kinds of forces: the electromagnetic force, the weak force, and the strong force. Together this description is called the Standard Model (SM) of particle physics. The energy evolution of the strength of these forces can be extrapolated to very high energies from their measured values at presently accessible energy ranges. Schematic representation of these extrapolations are illustrated on the left plot (figure 7) for the strength of electro-magnetic (aEM), weak (aW) and strong (aS) interactions.
|
|
| Fig 7. On the left, our current Standard Model, the strength of the forces come very close to each other at high energy. On the right, an unproven theory called supersymmetry predicts they all meet. |
It is of fundamental importance in our understanding
of the nature of particle interactions to determine if the strength of
these 3 forces converge to the strength of a single unifying force field
at very high energies: a hypothesis known as Grand Unification.
Measuring the strength of these interactions progressively, as higher and higher energy
scale becomes accessible to particle physicists at the high energy particle accelerators,
is thus a key measurement to unravel this unification.
Symmetry between different kinds of matter are necessary
to explain certain peculiarities of the high energy behavior of these interactions.
A very interesting symmetry between the fermions
(ie. particles with half-integer spin or equivalently with even number of polarization states)
and the bosons
(ie. particles with integer spin or equivalently with odd number of polarization states)
is called supersymmetry, which however must be broken
(as we do not yet see the super-partners).
This breaking is conjectured to happen at energy scales beyond the ones accessible
by present day particle accelerators.
The Minimal Supersymmetric Model (MSSM) makes concrete predictions
of sets of as yet unobserved particles, whose existence may completely change
our understanding of Nature. It also predicts that the extrapolation
for the strength of these interactions to very high energies may converge
as illustrated in the right plot of Figure 7.
Symmetry between different kinds of matter are necessary to explain certain peculiarities of the high energy behavior of these interactions. A very interesting symmetry between the fermions (ie. particles with half-integer spin or equivalently with even number of polarization states) and the bosons (ie. particles with integer spin or equivalently with odd number of polarization states) is called supersymmetry, which however must be broken (as we do not yet see the super-partners). This breaking is conjectured to happen at energy scales beyond the ones accessible by present day particle accelerators. The Minimal Supersymmetric Model (MSSM) makes concrete predictions of sets of as yet unobserved particles, whose existence may completely change our understanding of Nature. It also predicts that the extrapolation for the strength of these interactions to very high energies may converge as illustrated in the right plot of Figure 7.
It would be very interesting
to know if the strength of the particle interactions actually unifies
at very high energy! As yet, we can only measure in our experiments
a very small range of the energy toward the very left of the x-axis on the above plots,
but with more detailed understanding of the structure of matter, we would learn
how to extrapolate correctly to those high energies toward the very right of
the x-axis on the above plots.
Lets wait and see...
Lets wait and see...
University of Victoria, Canada
Currently based at SLAC
swaban@slac.stanford.edu